회귀 분석 포스팅 시리즈의 일환으로 다중 회귀 분석에 대해 정리해 보겠습니다.
다중 회귀 분석 (Multiple Linear Regression) 이란?
- 독립 변수 (Independent Variable) 가 여러 개로서 복합적으로 종속 변수에 영향을 미치는 회귀 분석을 의미합니다. 단순 선형 회귀 분석과 다른 점은 독립 변수가 여러 개 라는 것입니다.
- 변수 Y 에 원인이 되는 변수가 여러개(n) 포함되는 형태로 표현이 됩니다. 하기와 같은 방정식으로 표현이 됩니다.

- 여러 독립 변수 중에서도 종속 변수 에 영향을 주는 가장 중요한 변수가 무엇인지를 알 수 있습니다. 예를 들어, 하기 공식을 보면 자동차의 Co2 emission 에 대해 Cylinder 변수가 Engine size 보다 더 영향이 큼 을 알 수 있습니다.

- 다중 회귀 분석 역시 선형 회귀 분석과 마찬가지로 가장 최적화된 회귀선을 찾기 위해선 Mean Square Error 와 같이 에러 (실제 관측값 - 모델에 의한 예측값) 를 최소화 하는 방법을 사용합니다.
변수 선택
- 그렇다면 다중 회귀 분석에 어떤 독립변수를 추가할 것인지, 즉, 어떤 변수가 종속 변수 예측에 영향을 줄 것인지 어떻게 결정할 수 있을까요? 단순하게 무조건 많은 변수를 추가하는 것은 모델의 과적합성 (Overfitting) 을 증가시킬 수 있기 때문에 지양해야 합니다.
- 참고로, 범주(Categorical) 형 변수도 독립 변수로 선택할 수 있으며, 이 때 수치 변환을 해야 합니다.
- 우선 데이터셋을 Scatterplot (산점도) 으로 Plotting 해 본 후 선형 관계가 보이면 그 때 Linear Regression 을 적용해 볼 수 있습니다.
규제 적용
- 모델은 복잡도가 증가할 수록 과대적합 (Overfitting: 모델이 Train data 에만 매우 적합하고 실제 Test data 로 Validation 했을 때 예측률이 떨어지는 것) 이 발생할 수 있습니다. 그렇다면, 독립변수를 되도록 많이 포함하면서 모델 성능을 높일 수는 있을까요? 이를 위해 사용되는 것이 규제(Regularization) 입니다. 다중 회귀의 경우 여러 독립 변수들이 포함되므로 복잡도가 증가하여 규제 적용이 필요합니다.
- 규제를 적용하면, 각 피처의 가중치 (각 피처가 모델의 예측 결과에 미치는 영향력) 를 낮춤으로써 모델 구조의 복잡함을 억제할 수 있습니다. 가중치를 낮춘다는 말의 의미는 회귀식의 회귀 계수들을 0 으로 수축 시킨다고 이해할 수 있습니다.
- 모델의 복잡함을 낮추는 방법으로는 L2 규제와 L1 규제가 있는데, L2 규제는 가중치의 제곱합에 페널티를 부과하는 방법 이며, L1 은 가중치의 절대값의 합에 페널티를 부과하는 방법입니다.
- 규제에 대한 방법은 크게 릿지(Ridge), 라쏘(Lasso), 엘라스틱넷(ElasticNet) 이 있습니다.
| 규제 종류 | 설명 | 타입 | |
| L2 규제 | 가중치의 제곱합에 페널티를 부과 | 릿지(Ridge) | 엘라스틱넷(ElasticNet) (릿지와 라쏘의 절충) |
| L1 규제 | 가중치의 절대값의 합에 페널티를 부과 | 라쏘(Lasso) |
L2 규제로는 대표적으로 릿지(Ridge) 가 있고, L1 규제는 라소(Lasso) 가 있습니다. 하나씩 살펴 보겠습니다.
릿지 (Ridge Regression)
- 릿지 (Ridge Regression) 는 위에서 설명했듯, 과대적합을 방지하기 위한 알고리즘이며, 선형 회귀 모형에 L2 규제를 구현한 모델입니다. 즉, 가중치의 제곱합에 패널티를 부과 합니다.
- 이 때, 알파 (Alpha) 를 적용함으로 규제 강도를 조정합니다. 알파 값이 커지면 규제 강도가 세지고 모델의 가중치가 감소하게 됩니다. 알파가 0일 경우 패널티의 영향이 없어 릿지 회귀는 선형 회귀와 같은 양상을 보이나 알파가 커질수록 패널티의 영향이 커지고 회귀 계수 추정치는 0 에 가까워 짐으로써 각 변수의 가중치가 줄어듭니다.
- 예시를 살펴 보겠습니다. 하기 이미지의 회귀식은 매우 고차항의 다항식이기 때문에 회귀식을 그대로 적용할 경우 그만큼 y 예측에 있어 회귀 계수의 영향력이 높아지게 됩니다. 이럴 때 Alpha를 적용할 수 있습니다.

- 밑에 스크린샷을 보면, 왼쪽 표는 Alpha 값, 오른쪽 표는 각 항에 대해 Alpha 값 변화에 따른 계수 변화를 볼 수 있습니다.
- Alpha 가 커질수록 각 변수에 대해 회귀 계수는 작아짐을 확인할 수 있습니다. x10 항에 대해 알파가 0 이었을 땐 75 였던 계수가 알파가 0.01로 증가하나 1 로 줄어들었습니다. 그러나 Alpha 가 커질수록 계수가 작아져서 오히려 모델에 과소적합 (underfit) 해지는 현상이 발생할 수 있으므로 Alpha 값은 신중하게 선택 되어야 합니다.

- Alpha 값에 변화를 주면서 모델을 훈련 시키고 알파값을 달리한 각 모델에 대해 Training data 와 Test data 에 대해 R2 을 구해보는 (Cross Validation) 프로세스를 밟아 보았습니다. 하기 그래프는 그 결과입니다.
- 알파가 증가할수록 Training data 및 Test data 에 대해 r^2 이 어떻게 바뀌는지를 보여줍니다. alpha 가 증가할수록 overfitting 이 줄어드므로 Training data 는 r^2 이 다소 감소하고, Test data 에 대해서는 늘어남을 알 수 있습니다.

사이킷런(Scikit learn) 의 Ridge 함수 사용 예시
- 릿지를 실제로 적용해 보겠습니다. 릿지 역시 sklearn 에서 Ridge() 를 불러옴으로써 사용할 수 있습니다. 기본적인 메소드들은 다른 사이킷런의 알고리즘과 유사합니다.
- 주요 파라미터로는 Ridge() 안에 alpha 를 지정할 수 있습니다. default 값은 1 입니다.
- 속성으로는 coef_, intercept_ 이 있습니다. 선형 회귀에 대한 계수와 절편을 각각 출력합니다.
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
|
# Ridge 예시
from sklearn.linear_model import Ridge
ridge = Ridge(alpha = 2.5)
ridge.fit(X_train, y_train)
y_train_pred = ridge.predict(X_train)
y_test_pred = ridge.predict(X_test)
from sklearn.metrics import mean_squared_error
train_mse = mean_squared_error(y_train, y_train_pred)
print('Train data MSE:%.4f' % train_mse)
test_mse = mean_squared_error(y_test, y_test_pred)
print('Test data MSE:%.4f' % test_mse)
|
cs |
Ridge: 알파값(Alpha) 에 따른 회귀 계수(Coefficient) 변화 살피기
- 좀 더 예시를 보겠습니다. 이번엔 Ridge 함수에 알파를 각각 다르게 적용하여 회귀식의 회귀 계수가 어떻게 변화되는지 도출해보고 이를 시각화 로도 표현해 보겠습니다.
- 예시 데이터로는 사이킷런에서 제공하는 diabetes 데이터를 사용하겠습니다. (from sklearn.datasets import load_diabetes)
- 독립변수들을 데이터프레임으로 변환하고 출력해 보았습니다. 하기와 같이 10개의 변수입니다.

- 알파값을 총 5개, 0.001, 0.01, 0.1, 1, 10 이렇게 적용해 Ridge 함수를 만들고 훈련 데이터를 fit 해 보겠습니다.
- np.logspace() 를 이용하여 np.logspace(-3, 1, 5) 를 적용하면, 0.001, 0.01, 0.1, 1, 10 이렇게 5개의 숫자가 array 형태로 출력됩니다.
- 이를 for 문 및 enumerate 함수 에 적용하여 각 알파값을 Index 와 함께 iteration 시킵니다.
- Ridge 함수는 각 iteration 된 알파값이 적용되어 훈련 과정을 거칩니다. 이 때, 회귀식의 계수들은 data 라는 빈 리스트에 append 합니다. np.hstack 은 array 들을 합치는 함수입니다.
- 알파값이 0.001 일 때 각 항의 회귀 계수들을 포함하는 array 부터 10 일 때 각 항의 회귀 계수들을 포함하는 array 들이 합쳐지게 됩니다.
- 이 결과를 데이터프레임화 하여 df_ridge 에 저장합니다.
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
|
from sklearn.linear_model import Ridge
# =3 과 1 사이의 로그로 분할한 값으로 5개 출력
# (그러면 log10 을 기준으로 0.001, 0.01, 0.1, 1, 10 이렇게 5개 반환됨..) alpha = np.logspace(-3, 1, 5)
data=[]
# ridge 모델을 생성하되, alpha 값을 iteration 시켜서 여러개 대입 for i, a in enumerate(alpha):
ridge = Ridge(alpha = a, random_state = 45)
ridge.fit(X, y)
data.append(pd.Series(np.hstack([ridge.coef_])))
df_ridge = pd.DataFrame(data, index=alpha)
df_ridge.columns = X.columns
df_ridge
|
cs |
- df_ridge 의 인덱스는 Alpha값, 열은 각 변수명이며 각 데이터는 알파값, 각 항별 계수를 의미합니다. 알파가 커질수록 계수들이 줄어들고 있음을 알 수 있습니다.

- 위의 df_ridge 값을 비주얼라이제이션 해보겠습니다. 알파값 변화에 따라 계수들이 어떻게 주는지 시각화 해 볼 수 있습니다.
x축엔 Alpha, y축엔 계수, 범주(legend) 엔 각 칼럼, 즉 변수를 설정하겠습니다.
|
1
2
3
4
5
6
7
8
9
10
11
|
plt.semilogx(df_ridge)
plt.xticks(alpha, labels=np.log10(alpha))
plt.legend(labels=df_ridge.columns, bbox_to_anchor=(1, 1))
plt.title('Ridge')
plt.xlabel('alpha')
plt.ylabel('coefficient (size)')
# 가운데 y축 0 을 기준으로 dash line 추가가
plt.axhline(y=0, linestyle = '--', color='black', linewidth = 3)
plt.show()
|
cs |

- 참고로, plt.semilogx 는 x 축을 로그화 시키는 함수입니다. 특히 변수 데이터 간 range 가 차이가 많이 날 때 유용하며, 시각화 상에서 절대적인 차이를 완만하게 구현해 줍니다.

- 이번엔 다른 형태로 시각화 해보겠습니다. 각 feature 별로 알파값을 달리 적용할 때마다 계수가 어떻게 변화하는지 살펴 보겠습니다. 이번엔 x 축에 변수명을 범주를 ridge Alpha값으로 적용합니다. 규제가 적용되지 않은 일반 선형 회귀식도 불러와서 훈련을 시킵니다.
- 변수별로 알파값 변화에 따라 회귀 계수가 변동하는 정도를 한 눈에 알 수 있습니다.
- 알파값이 0.001 일 땐 일반 선형 회귀와 계수값이 거의 차이가 없으나, 알파값이 10 정도로 커지면 계수들은 0 에 꽤 가까운 모습을 보입니다. 이런 식으로 규제를 적용하면 회귀 계수들의 절대값은 0 에 좀 더 수렴한다는 것을 알 수 있습니다.
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
|
plt.axhline(y=0, linestyle='--', color='black', linewidth=2) # y축 0 기준으로 dash line
plt.plot(df_ridge.loc[0.001], '^-', label='Ridge alpha = 0.001')
plt.plot(df_ridge.loc[0.010], 's', label='Ridge alpha = 0.010')
plt.plot(df_ridge.loc[0.100], 'v', label='Ridge alpha = 0.100')
plt.plot(df_ridge.loc[1.000], '*', label='Ridge alpha = 1.000')
plt.plot(df_ridge.loc[10.00], 'o-', label='Ridge alpha = 10.00')
plt.plot(lr.coef_, label='LinearRegression') # alpha 가 0.001 에 가까움..
plt.xlabel('Feature Names')
plt.ylabel('Coefficient (Size)')
plt.legend(bbox_to_anchor=(1, 1))
plt.show()
|
cs |

- 알파(Alpha) 를 선택할 때, Cross-Validation 을 한 후 선택할 수 있습니다.
1) Cross validation 은 dataset 의 일부를 validation 으로 분류하고 시작한다. (Test Data 를 따로 빼는 것과 비슷한 개념)
2) 그리고 다양한 Alpha 값을 넣어보면서 -> 데이터를 Train 시키고 (Fit 함수)
3) 따로 빼둔 Validation 데이터로 prediction 을 한 후, Validation 데이터로 R^2 (결정계수) 값을 구해본다
4) 각 Alpha 값에 대한 결정계수를 각각 구해보고 비교한다. (예시, Alpha 가 0.5 일 때, 1일 때, 2일 때 등등에 대해 데이터를 Train 시키고 각각의 결정 계수를 구한다, 이 때 Python 의 Iteration 을 이용한다)
라쏘 (Lasso Regression)
- 라쏘(Lasso) 역시 규제의 일환으로 패널티를 부과하되 가중치의 절대값의 합에 패널티를 부과하여 모델의 복잡도를 낮추는 방식 (L1 규제) 입니다.
- 릿지의 경우, 특정 변수들을 모두 포함하며, 계수를 0으로 수렴시키지만 어떤 것도 0으로 만들지는 않습니다. 만약 변수의 크기가 매우 큰 데이터로 릿지 모델을 실행하면 결과적으로 어려움이 발생할 수 있습니다. 이럴 때는 라쏘가 더 대안이 될 수 있습니다.
- 릿지와 달리 라쏘는 계수 추정치들의 일부를 0 이 되게 할 수 있습니다. 즉, 특성 가중치를 제거할 수 있습니다.
사이킷런(Scikit Learn) 의 Lasso 함수 사용 예시
- 라쏘 역시 sklearn 에서 Lasso() 를 불러옴으로써 사용할 수 있습니다. 기본적인 메소드들은 다른 사이킷런의 알고리즘과 유사합니다.
- 주요 파라미터로는 Lasso() 안에 alpha 를 지정할 수 있습니다. default 값은 1 입니다. 알파값이 0일 경우 선형 회귀와 동등한 결과를 도출합니다.
- 속성으로는 coef_, intercept_ 이 있습니다. 선형 모델에 대한 대한 계수와 절편을 각각 출력합니다.
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
|
# Lasso 예시
from sklearn.linear_model import Lasso
lasso = Lasso(alpha = 0.05)
lasso.fit(X_train, y_train)
y_train_pred = lasso.predict(X_train)
y_test_pred = lasso.predict(X_test)
from sklearn.metrics import mean_squared_error
train_mse = mean_squared_error(y_train, y_train_pred)
print('Train data MSE:%.4f' % train_mse)
test_mse = mean_squared_error(y_test, y_test_pred)
print('Test data MSE:%.4f' % test_mse)
|
cs |
Lasso: 알파값(Alpha) 에 따른 회귀 계수(Coefficient) 변화 살피기
- 위 Ridge 에서 사용했던 동일한 diabetes 데이터를 사용하여 Lasso 를 적용하되, 알파값을 달리 했을 때, 회귀식의 회귀 계수가 어떻게 변화되는지 도출해보고 이를 시각화 로도 표현해 보겠습니다. Ridge 예시와 코드는 거의 유사하고, Lasso 를 불러온 차이 입니다.
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
|
from sklearn.linear_model import Lasso
import pandas as pd
# 0.001 부터 10 까지 10지수 로그 생성.. alpha 생성
alpha = np.logspace(-3, 1, 5)
# 빈 리스트 만들기 (data)
data = []
for i, a in enumerate(alpha):
# lasso 모델 부르기
lasso = Lasso(alpha=a, random_state = 45)
# alpha 리스트 내 각 알파값을 대입하여 모델 훈련시키기
lasso.fit(X, y)
# lasso.coef_ 값을 data 리스트에 붙여넣기 (append 가 시리즈도 어펜드가 가능한지 몰랐음..)
data.append(pd.Series(np.hstack([lasso.coef_])))
df_lasso = pd.DataFrame(data, index=alpha)
df_lasso.columns = X.columns
df_lasso
|
cs |
- 아래 스크린샷은 df_lasso 가 출력된 모습입니다. 하기 표의 index는 각 alpha값을 나타내며, 각 항별로 알파값에 따른 회귀 계수값의 변화를 보실 수 있습니다.

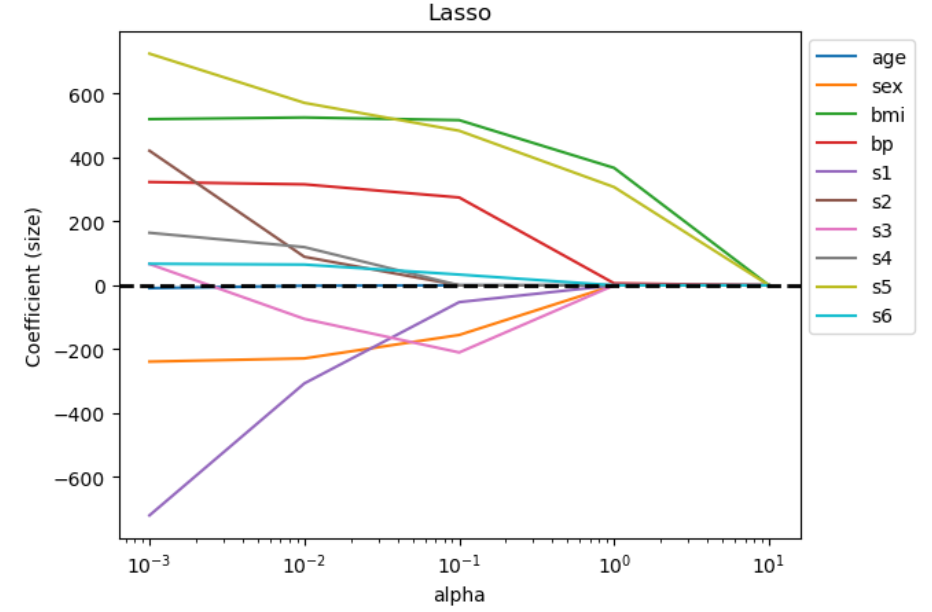
- 알파값이 커질수록 회귀 계수가 어떻게 변화하는지 살펴 보기 위해 df_lasso 를 시각화 해보겠습니다. 알파값이 커질수록 각 feature 는 0 에 수렴하는 모양을 보입니다.
|
1
2
3
4
5
6
7
8
9
10
11
|
plt.semilogx(df_lasso)
plt.xticks(alpha, label=np.log10(alpha))
plt.title('Lasso')
plt.xlabel('alpha')
plt.ylabel('Coefficient (size)')
plt.axhline(y=0, linestyle='--', color='black', linewidth=2)
plt.legend(labels=df_lasso.columns, bbox_to_anchor=(1, 1))
plt.show()
|
cs |
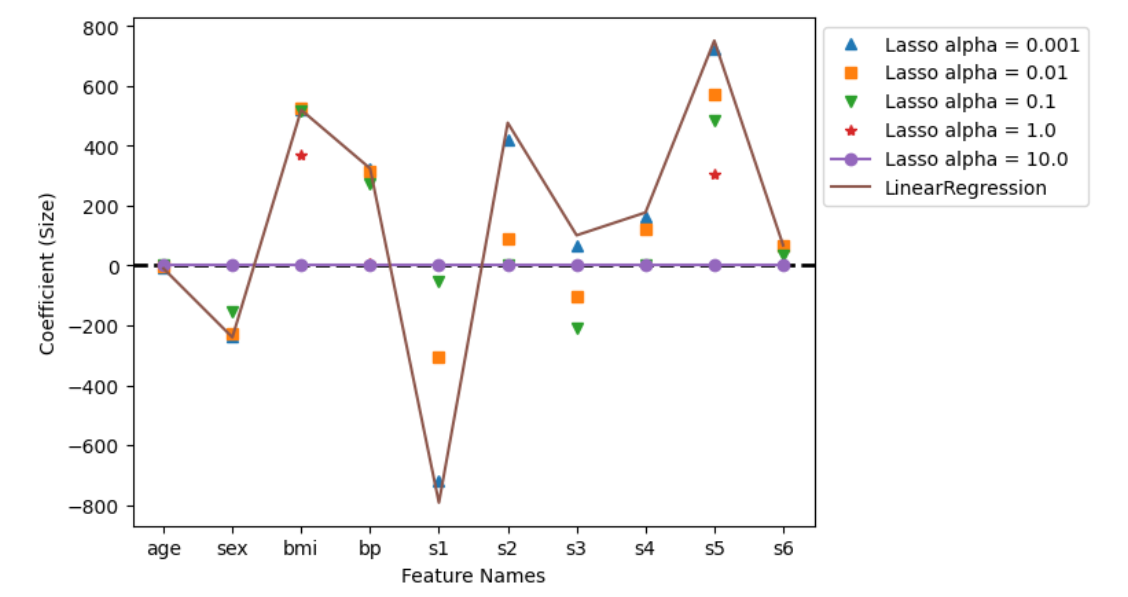
- 각 feature 별로 알파값을 달리 적용할 때마다 계수가 어떻게 변화하는지 다른 형태로 시각화 해보겠습니다. Ridge 에시와 마찬가지로 x 축에 변수명, 범주로 알파를 적용합니다. 규제가 적용되지 않은 일반 선형 회귀식도 같이 불러와 비교해 보겠습니다.
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
|
from sklearn.linear_model import LinearRegression
lr = LinearRegression()
lr.fit(X, y)
plt.axhline(y=0, linewidth=2, linestyle='--', color='black')
plt.plot(df_lasso.loc[0.001], '^', label='Lasso alpha = 0.001')
plt.plot(df_lasso.loc[0.010], 's', label='Lasso alpha = 0.01')
plt.plot(df_lasso.loc[0.100], 'v', label='Lasso alpha = 0.1')
plt.plot(df_lasso.loc[1.000], '*', label='Lasso alpha = 1.0')
plt.plot(df_lasso.loc[10.00], 'o-', label='Lasso alpha = 10.0')
plt.plot(lr.coef_, label='LinearRegression')
plt.legend(bbox_to_anchor=(1, 1))
plt.xlabel('Feature Names')
plt.ylabel('Coefficient (Size)')
plt.show()
|
cs |
- 역시 Ridge 처럼 Lasso 도 알파값이 커질수록 회귀계수의 절대값이 줄어드는 모양이나 Ridge 회귀식을 적용했을 때보다 좀 더 0에 수렴하는 차이가 있는 듯합니다. 알파값이 10 일 땐 심지어 모든 계수가 0 으로 수렴합니다.
참고자료>>
Evaluation Metrics in Regression Models - Regression | Coursera
Video created by IBM 기술 네트워크 for the course "Python을 통한 머신 러닝". In this module, you will get a brief intro to regression. You learn about Linear, Non-linear, Simple and Multiple regression, and their applications. You apply all th
www.coursera.org
https://medium.com/swlh/understanding-multiple-linear-regression-e0a93327e960
Understanding Multiple Linear Regression
A Guide for Beginners
medium.com
책: 엑셀을 활용한 마케팅 분석 기법
책: 빅데이터 분석기사 책 한권으로 끝내기 (SD 에듀, 시대고시기획)
책: 파이썬 딥러닝 머신러닝 입문 (정보 문화사, 저자: 오승환)
'데이터관련공부 > Machine Learning' 카테고리의 다른 글
| [데이터전처리] 데이터 분할 및 교차 검증 (Train, Test 데이터 분할, Cross Validation) (0) | 2023.12.21 |
|---|---|
| [분석알고리즘] 회귀 | 3. 다항 회귀 (Polynomial Regression) (0) | 2023.12.21 |
| [분석알고리즘] 앙상블 | 4. 보팅 (Voting) (0) | 2023.12.18 |
| [분석알고리즘] 앙상블 | 3. 부스팅 (Boosting) (0) | 2023.12.17 |
| [분석알고리즘] 앙상블 | 2. 배깅(Bagging) 및 랜덤포레스트 (Random Forest) (0) | 2023.12.17 |



